Lean Hamburrger est un restaurant fastfood servant des hamburgers parmi d’autres produits. Le restaurant affirme que la teneur moyenne en graisse des hamburgers est de 15 grammes.

Récemment, quelques clients se sont plaints auprès du responsable du fast food  que la teneur en graisse des hamburgers semblait être supérieure à celle de 15 grammes réclamée par le restaurant. Le responsable souhaite utiliser des intervalles de confiance de 95% pour vérifier si la réclamation du restaurant de 15 grammes (moyenne) de graisse dans les hamburgers est correcte. Il souhaite également vérifier son hypothèse selon laquelle l’écart type de la teneur en graisse est inférieur à 1 gramme.

Phase de mesure

On sélectionne au hasard 20 hamburgers et mesure la teneur en matières grasses (en grammes) dans chacun d’entre eux de la manière suivante: , 15,6, 13,5, 14,0, 16,5, 19,0 et 18,6.

Graisse
15,5
12,3
15,4
16,5
15,9
17,1
16,9
14,3
19,1
18,2
18,5
16,3
20
19
15,6
13,5
14
16,5
19
18,6

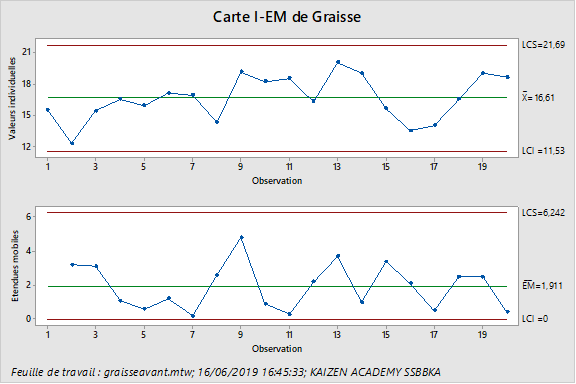
Il souhaite également vérifier si les données sont normalement distribuées avant de s’appuyer sur l’intervalle de confiance. Pour se faire

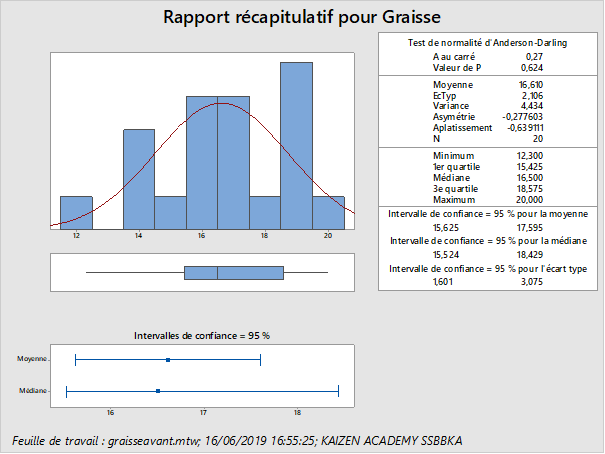
Test et limites de confiance pour 1 variance : Graisse

Méthode

σ: écart type de Graisse

La méthode de Bonett est valide pour toute loi de distribution continue.

La méthode du Khi deux est valide uniquement pour la loi normale.

Statistiques descriptives

N	EcTyp	Variance	Borne supérieure à 95% pour σ utilisant Bonett	Borne supérieure à 95% pour σ utilisant Khi deux
20	2,11	4,43	2,81	2,89

Avant de passer à la phase d’amélioration, le patron souhaite vérifier le nombre de clients insatisfaits. À cette fin, il sélectionne au hasard 1 000 clients qui ont acheté des hamburgers et constate que 83 d’entre eux sont mécontents de la qualité des aliments. Il construit ensuite un intervalle de confiance pour la proportion de tous les clients insatisfaits.

Test et IC pour 1 proportion

Méthode

p : proportion d’événement

La méthode de l’approximation selon la loi normale est utilisée pour cette analyse.

Statistiques descriptives

N	Evénement	P échantillon	Borne supérieure à 95% pour p
1000	83	0,083000	0,097350

Test

Hypothèse nulle	H₀ : p = 0,5
Hypothèse alternative	H₁ : p < 0,5

Test et IC pour 1 proportion

Méthode

p : proportion d’événement

La méthode de l’approximation selon la loi normale est utilisée pour cette analyse.

Statistiques descriptives

N	Evénement	P échantillon	Borne supérieure à 95% pour p
1000	83	0,083000	0,097350

Test

Hypothèse nulle	H₀ : p = 0,5
Hypothèse alternative	H₁ : p < 0,5

Phase d’analyse

Le patron analyse le processus et découvre que la teneur en graisse et ses variations sont fortement influencées par la quantité d’huile utilisée par les employés sur les trois différentes grilles utilisées pour la fabrication des hamburgers.

Phase d’amélioration

Le patron normalise le processus de sorte que l’utilisation de l’huile sur les trois différentes grilles soit contrôlée. Une machine automatique est achetée et installée pour distribuer de l’huile sur un gril chaque fois qu’un hamburger est fabriqué.

Afin de vérifier si le processus s’est vraiment amélioré, le responsable des opérations sélectionne au hasard 20 hamburgers et mesure la teneur en matières grasses (en grammes) dans chacun d’entre eux de la manière suivante:

14,9 15,0 15,4 15,3 15,2 15,1 14,9 14,8 15,6 14,5 15,3 15,8 15,0 15,0 14,3 15,3 15,2 14,7 15,1 14,7

On procède au test statistique suivant et on obtient les résultats suivants :

Test T à 2 échantillons et IC : avant; aprés

Méthode

μ₁ : moyenne de avant

µ₂ : moyenne de aprés

Différence : μ₁ – µ₂

Les variances ne sont pas supposées égales pour cette analyse.

Statistiques descriptives

Echantillon	N	Moyenne	EcTyp	ErT moyenne
avant	20	16,61	2,11	0,47
aprés	20	15,055	0,359	0,080

Estimation de la différence

Différence	IC à 95% pour la différence
1,555	(0,559; 2,551)

Test

Hypothèse nulle	H₀ : μ₁ – µ₂ = 0
Hypothèse alternative	H₁ : μ₁ – µ₂ ≠ 0

Valeur de T	DL	Valeur de P
3,26	20	0,004